
для решения / ТЕМА 3-5
.pdf
ТЕМА 3.5. Дискретные системы. Цифровые фильтры
Рассмотрим простейший, наиболее изученный и внедрённый класс систем дискретной обработки сигналов - линейные стационарные цифровые фильтры.
Выполняя, подобно аналоговым цепям, операцию частотной фильтрации, цифровые фильтры (ЦФ) обладают рядом существенных преимуществ. К ним относятся высокая стабильность параметров, возможность получать самые разнообразные формы АЧХ и ФЧХ. Цифровые фильтры не требуют настройки и легко реализуются на ЭВМ программными методами.
На рисунке 5.4 приведена структурная схема системы цифровой обработки сигналов.
|
|
|
|
|
Устройство |
|
Цифровой |
|
|
|||||
|
|
|
|
|
памяти |
|
|
|
|
|
Sвых(t) |
|||
S(t) |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Арифметическое |
|
|
|
ЦАП |
ФНЧ |
|
|||
|
|
|
|
|
устройство |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Синхронизатор
Рисунок 5.4 - Структурная схема цифровой обработки непрерывных сигналов
Непрерывный входной сигнал s(t) поступает в аналого-цифровой преобразователь (АЦП), управляемый синхронизирующими импульсами от генератора, задающего частоту дискретизации. Эта частота определяется в соответствии с теоремой Котельникова с учётом предварительных сведений о спектре ожидаемого (принимаемого) сигнала. В момент подачи синхронизирующего импульса на выходе АЦП возникает сигнал, отображающий результат измерения мгновенного значения входного колебания в виде числа (обычно в двоичном коде) с фиксированным количеством разрядов. В зависимости от особенности построения устройства этому числу соответствует либо последовательность коротких импульсов (единиц и нулей) в выходной шине (передача в последовательном коде), либо совокупность уровней напряжений на нескольких сигнальных шинах разрядов (передача в параллельном коде). В последнем случае количество шин определяется разрядностью кода. Использование параллельного кода обеспечивает более высокое быстродействие в обмен на аппаратурные затраты.
Преобразованный таким образом сигнал поступает в основной блок устройства, называемый цифровым процессором. Процессор содержит арифметическоеустройствоиустройствопамяти.Арифметическоеустройствопо заданному алгоритму выполняет над цифрами такие операции, как умножение, сложение и сдвиг во времени на заданное число интервалов дискретизации.
В устройстве памяти может храниться некоторое число предшествующих отсчётов входного и выходного сигналов, необходимых для выполнения выбранного алгоритма обработки.
Цифровой процессор преобразует поступающие в него числа в соответствии с заданным алгоритмом и создаёт на выходе последовательность двоичных чисел, представляющих выходной сигнал. Если в дальнейшем необходимо иметь информацию в аналоговой форме, то используется цифро-аналоговый преобразователь (ЦАП) и фильтр нижних частот.
Основной технический показатель ЦФ - быстродействие - зависит как от скорости протекания переходных процессов в микроэлектронных компонентах, так и от сложности алгоритма фильтрации. Достижения современной микроэлектроники непрерывно расширяют этот показатель. Цифровая фильтрация сигналов получила новый стимул развития с появлением относительно недорогих и надёжных микропроцессоров и устройств памяти.
ОстановимсянаквантованиисигналоввЦФ. Спецификалюбогоцифрового устройства – представление сигналов в виде последовательности чисел с ограниченной разрядностью. Поэтому мгновенное значение сигнала дискретизируется по уровню. Интервалом дискретизации по амплитуде (минимальной разностью между двумя соседними уровнями) служит единица младшего двоичного разряда.
Точное значение отсчёта сигнала в двоичной форме имеет вид
∞
X = ∑αn 2−n ,
n=0
где n = 0 или 1.
ПриограничениидлинычислаХнекоторымколичествомразрядовN вместо точного значения получается его округленное (машинное) представление:
X = N∑−1αn 2−n +βN 2−N ,
n=0
причём коэффициент βN равен либо n, либо n+1 в зависимости от того, нуль или единица содержится в (N+1)-м разряде.
Дискретные сигналы, уровни которых могут принимать лишь счётное множество значений, называют квантованными по уровню сигналами. Квантование сигналов приводит к специфической погрешности при обработке, которая получила название шума квантования. Прямой путь снижения этой погрешности – использование чисел с большим количеством разрядов. Однако при этом неизбежно снижается быстродействие ЦФ из-за увеличения времени выполнения операций. Обычно в микропроцессорных системах количество разрядов не превышает 16.
Итак, цифровая фильтрация предусматривает выполнение математи-ческих действий над отсчётами входного сигнала, преобразованными в цифровой код.
Алгоритм линейной фильтрации
Математическая теория цифровых фильтров переносит на случай дискретных сигналов все основные положения теории линейных систем, преобразующих непрерывные сигналы. Как известно, сигнал на выходе линейной стационарной системы у(t) равен свёртке входного сигнала s(t) и импульсной характеристики системы h(t):
∞
y(t) = ∫ s(τ)h(t −τ)dτ.
−∞
Цифровой фильтр есть дискретная система (физическое устройство или программа для ЭВМ), которая преобразует последовательность {sk} числовых отсчётов входного сигнала в последовательность {уk} отсчётов выходного сигнала:
(s0, s1, s2, ...)=>(у0, y1, y2, …), или {sn}=>{yk}.
Линейный цифровой фильтр обладает тем свойством, что сумма любого числа входных сигналов, умноженных на произвольные коэффициенты, преобразуется в сумму его откликов на отдельные слагаемые.
{xk(1)} =>{yk(1)} ,…, {хk(N)}=>{уk(N)}
или
α1{xk(1)}+…+αn{xk(N)} =>{α1yk(1)+…+αnyk(N)}.
при любых коэффициентах α1, α2, …, αn.
Импульсной характеристикой hk дискретного фильтра называется отклик
ЦФ на «единичный импульс» (1, 0, 0, 0, ...):
(1, 0, 0, 0, ... )=> (h0, h1, h2, ...).
Линейный ЦФ стационарен, если при смещении входного единичного импульса на любое число интервалов дискретизации импульсная характеристика смещается таким же образом, не изменяясь по форме:
(0, 1, 0, 0, ... ) => (0, h0, h1, h2, ... ), (0, 0, 1, 0, ... )=> (0, 0, h0, h1, h2, ... ).
Из свойств линейности и стационарности вытекает общий алгоритм линейной цифровой фильтрации. Пусть {sk} = (s0, s1, s2, ...) – некоторый сигнал на входе ЦФ с известной импульсной характеристикой. Используя предыдущие соотношения, m-й отсчёт выходного сигнала {yk} равен:
m
ym = s0hm + s1hm−1 +... + smh0 = ∑ sk hm-k .
k=0
Это выражение играет ведущую роль в теории линейной цифровой фильтрации. Оно показывает, что выходная последовательность дискретного линейного стационарного фильтра есть дискретная свёртка входного сигнала и импульсной характеристики фильтра. Смысл этого выражения прост и нагляден: каждый отсчёт выходного сигнала ЦФ является взвешенной суммой предыдущих значений входного сигнала, причём роль весовых коэффициентов играют отсчёты импульсной характеристики. Иными словами, ЦФ обладаетнекоторой «памятью» по отношению к прошлым входным воздействиям.
Дляфизическиреализуемыхфильтровкоэффициентыh-1, h-2, ...равнынулю, и суммирование распространяется только на положительные значения индекса k:
m
ym = ∑ sk hm-k , m = 0,1, 2, ... .
k=0
Чтобы перейти к частотной характеристике дискретного фильтра,
рассмотрим дискретные гармонические последовательности. Это комплексные сигналы вида
s (t ) = A e j(ωt +ψ),
отображающие гармонические колебания. При дискретизации такого сигнала по времени получается так называемая дискретная гармоническая последовательность:
{sk }={Ak exp(j(ωkT +ψ))},
такая, что
Re{sk }= Acos(ωkT +ψ).
Этипоследовательностипредставляютдискретизированныегармонические сигналынеоднозначно.Действительно,онипоследовательностинеизменятсяпри
замене частоты ω на ω+ 2Tnπ = ω+nωä где п – целое число, ωд – частота
дискретизации. Это связано с эффектом размножения спектра сигнала при квантовании.
Итак, алгоритм линейной цифровой фильтрации предусматривает выполнение цифровой свёртки сигнала и импульсной характеристики фильтра.
Характеристики дискретных фильтров
Рассмотрим характеристики дискретных фильтров.
Важнойхарактеристикойдискретногофильтраявляетсярассмотреннаявыше импульсная характеристика (отклик фильтра на «единичный импульс»
(1, 0, 0, 0, ...)).
Другой важной характеристикой дискретного фильтра является его частотный коэффициент передачи, или комплексная характеристика.
Пусть на вход линейного стационарного цифрового фильтра подана гармоническая последовательность {sk}, неограниченно протяжённая во времени, с индексом k, принимающим значения 0, ±1, ±2, ...
Сигнал на выходей фильтра {уk}, по формуле дискретной свёртки:
m |
m |
ym = ∑ sk hm-k = Aejψ |
∑ ejωkT hm-k . |
k=−∞ |
k=−∞ |
После замены переменных п = m – k и преобразования получим:
∞
ym = Ae j(ωmT +ψ) ∑ e−jωnT hn. n=0
Выходной сигнал, как и входной, имеет структуру дискретной гармонической последовательности с той же частотой, что и входной сигнал. Выходные отсчёты являются результатом умножения входных отсчетов на комплексную величину
∞
K ( jω) = ∑ e−jωnT hn ,
n=0
называемую частотным коэффициентом передачи ЦФ.
Из последнего выражения вытекают два замечания.
1. ЧастотныйкоэффициентпередачиЦФявляетсяпериодическойфункцией частоты с периодом, равным частоте дискретизации ωä = 2π/T .
2. Частотный коэффициент передачи есть дискретное преобразование Фурье импульсной характеристики ЦФ.
Специфической (присущей только дискретным фильтрам) является системная функция фильтра. Пусть дискретным сигналам {sk}, {yk}, {hk} соответствуют их Z-преобразования S(z), У(z), H(z) соответственно. Выходной сигнал фильтра {уk} есть свёртка входного сигнала и импульсной характеристики, поэтому выходному сигналу отвечает произведение их Z -преобразований:
Y (z)= S (z) H (z).
или
|
Y (z) |
∞ |
|
H (z) = |
= ∑hk z−k |
||
X (z) |
|||
|
k =0 |
Системной функцией фильтра H (z) называют отношение Z-преобразования
выходного сигнала к Z-преобразованию сигнала на входе.
Видно, что для получения частотного коэффициента передачи ЦФ из его
системной функции, в последней нужно сделать подстановку z = ejωT .
Итак, важнейшими характеристиками цифрового фильтра являются импульсная характеристика, частотный коэффициент передачи и системная функция фильтра. Эти характеристики однозначно связаны между собой и позволяют находить отклик фильтра на заданный сигнал.
Трансверсальные цифровые фильтры
Физически реализуемые ЦФ, которые работают в реальном масштабе времени, для формирования выходного сигнала в i-й дискретный момент времени могут использовать значение входного сигнала в момент i-го отсчёта, некоторое число «прошлых» входных отсчётов (xi-1, xi-2, …, xi-m), а также некоторое число предшествующих отсчётов выходного сигнала yi-1, yi-2, …, yi-n. Целые числа т и п определяют порядок ЦФ. Классификация ЦФ проводится в зависимости от того, как используется информация о прошлых состояниях системы.
Трансверсальные ЦФ. Так принято называть фильтры, которые работают в соответствии с алгоритмом
yi = ao xi +a1xi −1 +...+am xi −m ,
где a0, а1, а2, …, am – коэффициенты фильтра; т - порядок фильтра.
Как видно из этого выражения, трансверсальный фильтр проводит взвешенное суммирование т предшествующих отсчётов входного сигнала и не использует отсчёты выходного сигнала.
Применив Z-преобразование к обеим частям последнего выражения, убеждаемся, что
yi = ao xi +a1xi −1 +...+am xi −m.
Отсюда следует, что системная функция
H (z) = ao + a1z−1 +... + am z−m = ao zm + a1zm−1 +... + am zm
является дробно-рациональной функцией переменной z, имеющей m- кратный полюс при z = 0 и т нулей, координаты которых определяются коэффициентами фильтра аi.

Алгоритм функционирования трансверсального ЦФ поясняется структурной схемой, приведенной на рисунке 5.5 (слева – общий вид, справа – фильтр первого порядка).
Основными элементами фильтра служат блоки задержки отсчётных значений на интервал дискретизации (прямоугольники с символами z-1), а также масштабные блоки, выполняющие умножение на соответствующие коэффициенты аi. С выходов масштабных блоков сигналы поступают в сумматор, где, складываясь, образуют отсчёт выходного сигнала.
xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
-1 |
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
Z |
|
|
Z |
|
|
|
xk |
+ |
|
yk |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ao |
|
|
a1 |
|
am-1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Z-1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yk |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Сумматор |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 5.5 – Структурная схема трансверсального ЦФ Cтруктурная схема, изображенная на рисунке, не является принципиальной
схемой электрической цепи, а служит лишь графическим изображением алгоритма обработки сигнала. Используя средства языка программирования, можно составить программу, реализующую трансверсальную цифровую фильтрацию.
Импульсную характеристику трансверсального ЦФ найдем путем логических рассуждений. Если на вход фильтра подать одиночный импульс единичной амплитуды - «единичный импульс» (1, 0, 0, ...), на выходе фильтра поочередно будут появляться отсчеты, прошедшие линии задержки и усилители. Следовательно, импульсная характеристика является последовательностью весовых коэффициентов фильтра:
hk = (a0 , a1, a2 , ... , am ).
К аналогичному результату можно прийти строго, осуществив обратное Z- преобразование приведенной ранее системной функции фильтра Н{z}.
Важно, что импульсная характеристика трансверсального фильтра содержит конечное число членов.
Найдем системную функцию фильтра. Для этого применим Z- преобразование к импульсной характеристике. Получим:
H (z) = a |
|
+a z−1 +...+a |
|
z−m = |
a |
|
zm +a zm−1 |
+...+a |
|
|
|
|||
o |
m |
|
o |
1 |
|
m |
|
|
||||||
|
|
1 |
|
|
|
|
|
zm |
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если в |
|
последней формуле |
провести замену переменной z = e jω∆ , то |
|||||||||||
получим частотный коэффициент передачи фильтра: |
|
|
||||||||||||
K(jω)= a |
0 |
+a e− jω∆ +a |
2 |
e− j2ω∆ + |
... +a |
m |
e− jmω∆. |
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
Призаданномшагедискретизации можно реализовать разные АЧХ, меняя весовые коэффициенты фильтра.
Итак, трансверсальный фильтр проводит взвешенное суммирование предшествующих отсчётов входного сигнала и не использует отсчёты выходного
сигнала. Подбирая весовые коэффициенты фильтра, можно придать желаемую форму его АЧХ.
Рекурсивные цифровые фильтры
Этот вид цифровых фильтров характерен тем, что для формирования i-гo выходного отсчёта используются предыдущие значения не только входного, но и выходного сигнала:
yi = ao xi +a1xi −1 +...+am xi −m +b1 yi −1 +b2 yi −2 +...+bn yi −n ,
причём коэффициенты b1, b2, ... , bn, определяющие рекурсивную часть алгоритма, не равны нулю одновременно.
Чтобы подчеркнуть различие структур двух видов ЦФ, трансверсальные фильтры называют также нерекурсивными.
Найдем cистемную функцию рекурсивного ЦФ. Выполнив Z- преобразование обеих частей предыдущего рекуррентного соотношения, получим:
|
Y(z) |
a |
o |
+a z−1 |
+...+a |
m |
z−m |
|
a |
o |
zn +a zn−1 |
+...+azn−m |
. |
||
H (z) = |
|
= |
|
1 |
|
|
= |
|
1 |
|
|
||||
X (z) |
|
1−b1z−1 −...−bn z−n |
|
|
zn −b1zn−1 |
−...−bn |
|
||||||||
Функцияимеетнаz-плоскостиn полюсов.Есликоэффициентырекурсивной части алгоритма вещественны, то эти полюсы либо лежат на вещественной оси, либо образуют комплексно-сопряженные пары.
На рисунке 5.6 изображена структурная схема рекурсивного ЦФ (слева – общий вид, справа – фильтр первого порядка с нулевым порядком трансверсальной части). Верхняя часть схемы отвечает трансверсальной (нерекурсивной) части алгоритма фильтрации. Для её реализации требуется в общем случае т + 1 масштабных блоков (операций умножения) и т ячеек памяти (линий задержки), в которых хранятся входные отсчёты. Рекурсивной части алгоритма соответствует нижняя часть структурной схемы. Здесь используются п последовательных значений выходного сигнала, которые в процессе работы фильтра перемещаются из ячейки в ячейку путем сдвига.
xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Z |
-1 |
|
|
|
|
|
Z |
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
ao |
|
|
|
|
|
a1 |
|
|
|
|
am-1 |
|
|
|
|
|
yk |
|
+ |
|
|
|
yk |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Сумматор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bn-1 |
|
|
|
|
|
b2 |
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
-1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z-1 |
|
|
|
|
|
|
|
|
Z-1 |
|
|
|
|
|
Z-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рис. 5.6. Структурная схема рекурсивного ЦФ. Рекурсивный ЦФ является системой с обратной связью и может быть
неустойчив. Если заданы некоторые начальные условия, т. е. совокупность значений yi-1, yi-2, ... , yi-n, в отсутствие входного сигнала на выходе фильтра
образуются элементы бесконечной последовательности yi, yi+1, yi+2, …, играющей роль свободных колебаний.
Цифровой фильтр называется устойчивым, если свободный процесс есть невозрастающаяпоследовательность, т. е. |уn|приn => ∞непревышаетнекоторого положительного числа М независимо от начальных условий.
Если все полюсы системной функцииH(z) (числа z1, z2, …, zn) по модулю не превосходят единицы, располагаясь внутри единичного круга с центром в точке z = 0, то любой свободный процесс в ЦФ будет описываться убывающей геометрической прогрессией и фильтр будет устойчив.
Итак,врекурсивномфильтреиспользуютсяпредыдущиезначениянетолько входного, но и выходного сигнала. Рекурсивный фильтр устойчив, если все полюсы его системной функции H(z) по модулю не превосходят единицы.
Математическая теория цифровых фильтров является частным случаем теории фильтрации применительно к дискретным сигналам. Любой аналоговый фильтр может быть представлен следующий математической моделью:
∞
y(t) = ∫x(τ)h(t −τ)dτ , (4.2)
0
где x(τ) - входной сигнал;
h(t −τ) - импульсная характеристика аналогового фильтра;
t −τ - интервал времени между моментом t появления выходного сигнала, соответствующего x(τ) , и моментом прихода собственно x(τ) .
Для линейных дискретных систем, каким являются цифровые фильтры, выражение (4.2) примет следующий вид:
∞
y(n) = ∑x(m) h(n − m),(4.3)
m=0
где x(m) и h(n − m) соответственно дискретные отсчеты входного сигнала и импульсной характеристики.
Для физически реализуемых фильтров все h(n − m), для которых
n −m < 0, равны нулю. Это означает, что выходной сигнал цифрового фильтра в n −й момент времени является взвешенной суммой всех предыдущих входных воздействий.
Импульсная характеристика ЦФ представляет собой результат дискретизации с периодом Тд импульсной характеристики некоторого
аналогового фильтра прототипа, обладающего такой же амплитудно-частотной характеристикой (АЧХ). Чем меньше период дискретизации, тем ближе АЧХ цифрового фильтра и АЧХ аналогового фильтра-прототипа. Кроме того, АЧХ
цифрового фильтра будет периодической функцией с периодом ωд , поэтому о подобии АЧХ можно говорить лишь для интервала частот:
|
|
π |
<ω < |
|
π |
, |
|
|
Тд |
|
, |
||||
|
|
Tд |
|||||
− |
ωд |
<ω < |
ωд . |
|
|||
|
2 |
|
2 |
|
|
||
Выражение (4.3) может быть представлено в следующем виде:
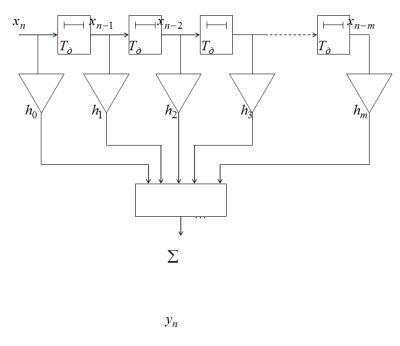
yn = h0 xn + h1xn−1 + h2 xn−2 +... + hmxn−m .(4.4)
Вреальных устройствах число слагаемых ограничено, параметр m, характеризующий эти ограничения, называется порядком фильтра.
Фильтр, реализующий выражение (4.4), называется нерекурсивным или трансверсальным. Реализация такого фильтра на дискретных элементах приведена на рисунке 4.3.
Всостав структурной схемы фильтра (рисунок 4.3) входят: элементы памяти (элементы задержки на период дискретизации); масштабные блоки, выполняющие в цифровой форме операции умножения на соответствующие коэффициенты; многовходовый сумматор, осуществляющий сложение полученных отсчетов. Структурная схема является графическим изображением алгоритма (4.4), который может быть легко записан в виде программы. Для этого
воперативной памяти ЦВМ образуются два массива длиной m: массив X (для хранения m- отсчетов входного сигнала) и H (для хранения масштабных
коэффициентов hi ).
Рисунок 4.3 – Нерекурсивный цифровой фильтр на дискретных элементах
Содержание ячеек массива X меняется каждый раз с получением нового отсчета входного сигнала, то есть новый отсчет записывается в ячейку 1, а данные, которые были записаны в ней, должны быть переписаны в ячейку 2, данные ячейки 2 сдвигаются в ячейку 3 и т.д. Элементы массива X почленно умножаются на элементы массива H , суммируются, результат накапливается в массиве Y. Таким образом, на каждый такт дискретизации на выходе накопителя
реализуется отсчет выходного сигнала yn .
Кроме трансверсальных фильтров широко используются также рекурсивные фильтры. Для рекурсивных фильтров соотношение между входной
последовательностью {x(n)} и откликом фильтра {y(n)} может быть записано следующим образом:
y(n) = F[y(n −1), y(n − 2),..., x(n), x(n −1),...],
т.е. текущий отсчет отклика y(n) определяется не только текущим и
предшествующими значениями входной последовательности, но и предшествующими отсчетами отклика.
Как уже отмечалось, Z - преобразование любой линейной дискретной системы, в том числе и цифрового фильтра, можно выразить в виде дробно-
рационального полинома по переменной Z−1, т.е.
|
|
N |
|
H (Z) = Y(Z) |
|
∑aiZ−i |
, (4.5) |
= |
i=0 |
||
N |
|
||
X(Z) |
|
|
|
|
∑b Z−i |
|
|
|
|
i |
|
|
|
i=0 |
|
причем b0 =1.
Предположение о равенстве степени числителя и знаменателя обязательным не является, а служит лишь для упрощения дальнейших выводов.
Приведя равенство (4.5) к общему знаменателю, получим:
N −i
Y(Z) ∑biZ
i=0
или
N −i
∑biZ Y(Z)
i=0
N −i ,
=X(Z) ∑aiZ
i=0
N −i .(4.6)
= ∑aiZ X(Z)
i=0
Если рассматриватьчлены вида Z−kY(Z) как обратные Zпреобразования
последовательностей y(n − k),то,взявобратные Z преобразованияобеихчастей равенства (4.6), можно получить искомое разностное уравнение:
N |
N |
∑bi y(n −i) = |
∑aix(n −i) . (4.7) |
i=0 |
i=0 |
Поскольку b0 =1, уравнение (4.7) можно решить относительно y(n):
N |
N |
y(n) = ∑aix(n −i) − ∑bi y(n −i) . (4.8) |
|
i=0 |
i=1 |
По аналогии с реализацией выражения (4.4) структурная схема рекурсивного фильтра по выражению (4.8) примет вид, показанный на рисунке
4.4.
