ТЕМА 1.1. Общие сведения о сигналах и их спектральный анализ

В процессе работы любого радиотехнического устройства или системы происходят преобразования сигналов. Некоторое из этих преобразований являются типовыми для большинства радиотехнических систем независимо отих назначения. При этом главным требованием к процессу передачи и приема сообщений является сохранение заключенной в этих сообщениях информации.

С точки зрения терминологии под информацией понимают совокупность разнообразных сведений, которые люди получают в процессе общения между СОБОЙ и природой. Сообщение, выступающее в виде письма, речи, изображения, цифровых данных и т.д. является информацией. Обмен информацией обычно осуществляется путем непосредственной передачи сообщений или с помощью сигналов.

С и г н а л о м называется некоторой физический процесс, однозначно отображающий информацию и пригодный для передачи на расстояние. К числу таких процессов относятся, например, звуковые колебания, электрические колебания (напряжение или тег при передаче сообщений яр проводам), а также электромагнитные колебания - радиоволны или оптическое излучение.

В радиотехнике сигналы того или иного назначения передаются от отправителя к получателю без проводов. С этой целью радиотехника использует свободно распространяющееся в пространстве электромагнитное поле.

Электромагнитное поле - это вид материи, определяющийся во всех точках двумя векторными величинами, которые характеризуют две его стороны, называемые соответственно "Электрическое поле" и "Магнитное поле", оказывающий силовое воздействие на заряженные частицы, зависящее от их скорости и величины их заряда.

Электромагнитное поле обладает замечательной особенностью. Будучи создано в пространстве, оно не может оставаться в покое, а обязательно приходит в движение с весьма большой скоростью, параметрами среды. Электромагнитное поле, распространяющееся в пространстве с определенной скоростью называется

э л е к т р о м а г н и т н о й в о л н о й.

1

Из курса физики известно, что эффективное излучение электромагнитных волн можно осуществить лишь при условиях, что геометрические размеры излучаемой системыантенны соизмеримы с длиной волн.

Может возникнуть вопрос, нельзя ли для передачи человеческой речи помощью радиоволн превратить звуковые колебания в электронные,а последние с помощью антенны преобразовать в электромагнитные волны, чтобы затем в приемном пункте эти электромагнитные волны снова превратить в звуковые.

Колебания, создаваемые голосом, являются колебаниями низких частот, лежащихобычнопределахот75до3000Гц.Такиечастотысоответствуютдлинам волн от 4000 до 100 км. Примерно такие размеры должны иметь передающая и приемная антенны. Антенны как указывалось выше, могут эффективно излучать электромагнитные колебания только тогда, когда их размеры соизмеримы с длиной волны. Поэтому передача колебаний звуковых частот оказывается практически невозможной.

Если учесть, что можно построить антенны с размерами, не превышающими несколько сотен метров, то становится ясным, что для радиосвязи можно использовать электромагнитные волны длиной не более нескольких километров. Они будут соответствовать частотам, во много раз превышающим частоты звуковых колебаний. Колебания таких частот используются в качестве носителя полезных ЗВУКОВЫХ, например, сигналов и называются несущими колебаниям. "Нагружают" несущее колебание информацией путем изменения его амплитуды, частоты или фазы по закону передаваемого сообщения. Процесс изменения параметров несущего колебания называют модуляцией. Радиосигналом называют высокочастотное электрическое колебание, у которого один иди несколько параметров изменяются по закону передаваемого сообщения.

Таким образом, всякое радиопередающее устройство должно иметь четыре обязательных элемента: преобразователь сообщения в электрический сигнал (микрофон, передающая телевизионная трубка, телеграфный ключ и др.), модулирующее устройство, передающую антенну (рис.1).

Рис. 1

В приемном пункте должно находиться устройство, преобразующее энергию электромагнитных волн в энергию электрических колебаний, т.е. приемная антенна. К антенне, расположенной в приемном пункте, приходят электромагнитные волны, излучаемые разными источниками и на различных частотах. Для того, чтобы принимать сигналы только одной радиостанции, необходимо иметь избирательное устройство, способное выделить или отфильтровать из колебаний различных частот только те колебания, которые передаются нужной радиостанцией. Для решения этой задачи может использоваться,например,электрическийколебательныйконтур,настроенныйна частоту принимаемой радиостанции,

2

Заметим, что термин «видео» в этом контексте совсем не подразумевает отношения сигнала именно к телевизионной технике. Смысл термина выяснится

входе дальнейшего изложения.

•финитный сигнал (треугольный видеоимпульс):

• периодический сигнал:

k =−∞

где r(t) — финитный на интервале Т (периоде последовательности) сигнал; иногда говорят о «представительном» сигнале последовательности.

• дискретный сигнал, являющийся последовательностью отсчетов (чисел):

Тестовые сигналы.Особое место средиматематических моделей сигналов занимают модели тестовых, испытательных или пробных сигналов. Они широко используются в теоретических исследованиях, а приближенно отвечающие им физические (радиотехнические) сигналы — в экспериментальной радиотехнической, радиоизмерительной практике.

Известным тестовым сигналом является единичная ступенчатая функция,

функция включения, или функция Хевисайда:

Важнейшим тестовым радиотехническим сигналом является дельтафункция, или функция Дирака δ(t) , которая определяется соотношениями

Из первой части определения (1.9) следует, что δ(t) существует лишь при аргументе t = 0, поэтому справедливо:

размерности аргумента t Отметим также важное соотношение, определяющее

фильтрующее свойство δ -функции:

−∞

4

т. е. определенный интеграл, подынтегральная функция которого содержит в качестве сомножителя δ -функцию, равен значению этой функции с аргументом, при которомδ -функция не равна нулю.

Функция δ(t) относится к так называемым обобщенным, символическим

функциям. С ее помощью, например, определяют не существующую в классическом смысле производную функции Хевисайда

Тестовыми являются гармонический сигнал (1.1) и гармоническая (квазигармоническая) функция включенияs(t) cosω0t,t ≥ 0 , которую, используя

функцию Хевисайда, можно записать как s(t) =Uσ(t) cosω0t .

Радиосигнал. Так называют сигнал, модель которого удобно представлять в форме

Выделяют огибающую U(t) полную фазу радиосигнала ψ(t) и фазовую функцию ϕ(t) Частоту ω0 = 2πf0 называют несущей частотой. Используя модель (1.14), обычно предполагают, что огибающая U(t) и фазовая функция ϕ(t) изменяются за время T0 = 2π / ω0 (период несущей частоты) незначительно (если

это предположение не выполняется, то может оказаться удобнее иная форма представления сигнала). Очевидно, что представления многих сигналов могут рассматриваться как частные случаи выражения (1.14), например, при U(t) = U = const, или при ω0 = 0, или при ϕ(t) = 0 и т. д. В последнем случае, т.е. если ϕ(t) = 0 ,

то ϕ0 называют начальной фазой.

Простейшим радиосигналом является гармоническая функция (1.1). Если огибающая U(t) — финитная функция, то радиосигнал (1.14)

называют радиоимпульсом, огибающую U(t) — соответствующим ему видеоимпульсом, а ω0 — частотой заполнения радиоимпульса (приϕ(t) =ϕ0 ).

Выбрав в качестве огибающей прямоугольный видеоимпульс (1.4) и положив ϕ(t) =ϕ0 = 0 , получим радиосигнал в виде прямоугольного радиоимпульса

S(t) = U cosω0 ,t [−T / 2,T / 2], (1.15)0, t [−T / 2,T / 2].

Если огибающая U(t) — непрерывная функция, определенная на интервалах t (−∞, ∞) или t (−∞, ∞) , то ее иногда называют видеосигналом,

соответствующим радиосигналу (1.14).

Гармонический анализ периодических сигналов

Для анализа сигналов очень важны методы представления математической модели сигнала в виде разложения ее в функциональный ряд. Функциональные ряды широко используются при решении многих задач физики и математики.

Тригонометрический, гармонический ряд ИЛИ ряд Фурье занимает среди них

5

особое место. Для радиотехнических приложений важность разложения сигнала по ортогональной гармонической системе функций определяется, в частности, тем, что, во-первых, такое разложение оказывается безусловно применимым как для сигналов, модели которых заданы единым аналитическим выражением, так и для сигналов кусочно-заданных несколькими аналитическими выражениями; вовторых, характером преобразования, которое претерпевает сигнал (1.1) при прохождении через стационарную линейную (например, RLC) цепь; как известно, выходным сигналом в этом случае является гармонический сигнал с той же круговой частотой со0, отличающийся от входного амплитудой и фазовым сдвигом. Если разложение входного сигнала по ортогональной системе тригонометрических функций известно, то выходной сигнал может быть получен как сумма независимо преобразованных цепью входных гармоник.

Тригонометрическая форма рада Фурье. Будем считать известным [3],

∞

что периодический сигнал (1.6) sr (t) = ∑r(t − kT ), k = ±1,±2,..,

k =−∞

определенный на бесконечном интервалеt (−∞, ∞) , может быть представлен в виде ряда Фурье:

гдеω1 = 2π / T = 2πf1, f1 =1/ T и k =1,2,.... Установлено, что разложение (1.16) существует, если r(t) на периоде Т удовлетворяет условиям Дирихле:

•не имеет разрывов 2-го рода (с уходящими в бесконечность ветвями функции);

•имеет конечное число разрывов 1-го рода;

•имеет конечное число экстремумов.

Коэффициенты ак (включаяa0 ) и bk определяются формулами

Иногда удобнее вычислять a0 / 2 не по общему выражению для <%

полученному в результате интегрирования, а положив к = 0 непосредственно в

(1.17):

В радиотехнической практике часто оказывается удобнее иное представление ряда (1.16). Проделав элементарные преобразования:

получим представление сигналаSr (t) в виде ряда Фурье в вещественной форме:

6

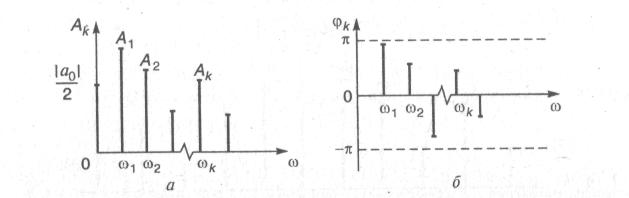
и коэффициентов Ак в (1.19) образует амплитудный, а совокупность ϕk — фазовый спектры периодического сигнала sr (t) .Возможный их вид показан на

рис. 1.1, а, б соответственно.

Комплексная форма ряда Фурье. Воспользовавшись формулами Эйлера

ряд (1.16) можно записать в виде:

Введем комплексные амплитуды

и «отрицательные» частоты ω−k = −kω1 = −ωk , т. е. включим в область изменения k значения к < 0 и запишем (1.16) в виде:

Рис. 1.1. Возможный вид амплитудного (а) и фазового (б) спектров периодического сигнала

Это представление называют комплексной формой ряда Фурье. Если дополнительноввестиобозначениеСо = Со = ао/2,рядФурьевкомплекснойформе можно записать лаконичнее:

k=−∞

Целесообразность введения комплексной формы ряда Фурье обусловлена удобством выполнения математических преобразований и некоторыми другими обстоятельствами.

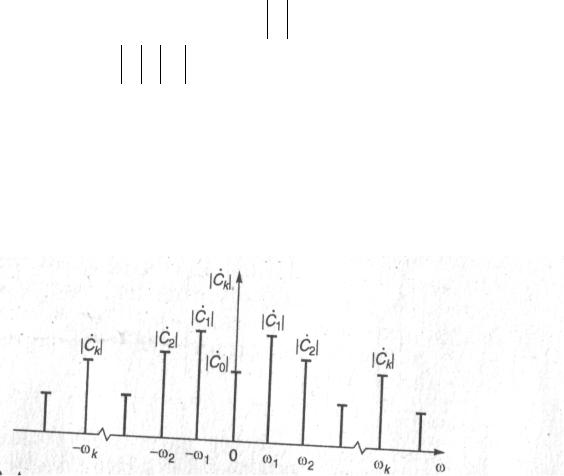
Коэффициенты ряда (1.21) Ск образуют дискретный комплексный спектр периодического сигнала sr (t), определенный на всех частотах ωk , к = 0, ±1, ±2, ...

7

возможный вид амплитудного спектра C.k .

Очевидно, что С.k = C.−k = Ck = Ak / 2.Рассмотрим ряд (1.21) подробнее:

Сопоставив выражения (1.17) и (1.20), замечаем, что

Рис. 1.2 Амплитудный спектр периодического сигнала при использовании комплексной формы ряда Фурье

Формула (1.22) используется для непосредственного вычисления

С. k , k = ±1,±2,....

Замечание 1

Пределы интегрирования в выражениях (1.17) и (1.22) могут быть изменены; существенно лишь то, что интегрировать следует по интервалу, равному полному периоду, например, от —Т/2 до Т/2 или от –Т до 0 и т. д. Это связано с тем, что для периодической с периодом Т функции f(t) значение определенного интеграла

λ+T

∫ f (t)dt

λ

не зависит от λ . Это соображение иногда оказывается полезным при практических вычислениях. Например, рассматривая (1.17) при симметричных пределах интегрирования от —Т/2 до Т/2, легко видеть, что ряд (1.17) будет содержать: в случае четности функции sr (t) лишь косинусоидальные члены с

коэффициентами ak ; в случае нечетности функцииsr (t) лишь синусоидальные члены с коэффициентами bk — независимо от того, какие пределы

8

интегрирования будут реально выбраны при вычислении коэффициентов ak и bk

.

Замечание 2

Подчеркнем эквидистантность спектра Фурье: частоты, на которых расположены коэффициенты ряда, образуют эквидистантную последовательность (... − 2ω1 , −ω1 , 0, ω1 , 2ω1 , 3ω1 , ...), непременно содержащую ω

= 0 и имеющую шаг ω1 = 2π / T . Сами же коэффициенты могут принимать любые,

в том числе и нулевые, значения.

Замечание 3

ПриобсуждениивопросовразложенияпериодическогосигналаврядФурье упоминаласьортогональностьсистемыфункций,покоторойведетсяразложение

[1].

Напомним определение ортогональности системы функций: бесконечная

Спектры некоторых периодических сигналов

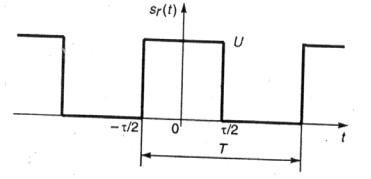
Последовательность прямоугольных видеоимпульсов. Рассмотрим спектр сигнала, изображенного на рис. 1.3. Такой сигнал часто используется в различных радиотехнических приложениях, а его модель — в теоретической радиотехнике.

Аналитическое представление сигнала на интервале Т (представительный

Введено обозначение длительности прямоугольного импульса τ

.Воспользуемся комплексной формой ряда Фурье (1.21):

Рис. 1.3. Последовательность прямоугольных видеоимпульсов

9